Anyone who thinks there is a simple answer to that question will be seriously disappointed. What have famous mathematicians said about it?
Mathematics is the art of giving the same name to different things (Henri Poincaré)
Thus mathematics may be defined as the subject in which we never know what we are talking about, nor whether what we are saying is true (Bertrand Russell)
Is mathematics something ‘out there’ waiting to be discovered, or is it a product of the human mind? Do we discover mathematical laws and relationships in nature, or do we impose mathematical descriptions on nature as a way of making sense of it, and harnessing it? Do we even know what number and arithmetic are? Yes, we all know what five loaves and three fishes are because those numbers have referents, but what of the number ‘three’ apart from its being a word or a symbol – does it exist as an immaterial entity? If so, where?
Questions such as these have interested philosophers and mathematicians for centuries. There are at least three fundamental questions to be addressed, on ontology, epistemology, and truth:
- What is the nature of mathematical objects?
- How do we obtain knowledge of them?
- How do we account for certitude in mathematics?
We could add another question on effectiveness:
- How do we account for the utility of mathematics in physics?
The various views on these questions correspond to the two camps of the medieval philosophers, the Realists and the Nominalists (or Anti-Realists), though Realism goes back much further to ancient Greece. Essentially, Realists believe that abstract entities or universals exist in their own right independently of the mind that thinks them, whereas Nominalists deny the extra-mental reality of universals and abstract ideas.
At the one extreme we have the ancient Pythagoreans who identified mathematics with reality itself. Number was ultimate reality. Then we have the Platonists who had their world of ideas and forms, which later Christian philosophers such as Augustine would locate in the mind of God. Galileo marks a shift from Christian Platonism back to Pythagoreanism, for he spoke of mathematics as being the language of nature. Descartes pushed things further in that direction, and with Newton, the Enlightenment, and the Deists the universe became a vast mechanical machine, the totality of motions of objects in space and time mathematically expressible in classical physics and Euclidean geometry, and all understandable by human reason.
As is well known, such a notion was abandoned in the early Twentieth century with the rise of quantum physics and relativity, and following the ‘discovery’ of non-Euclidean geometries in mathematics in the Nineteenth century. Bertrand Russell remarked
It has gradually appeared, by the increase of non-Euclidean systems, that Geometry throws no more light on the nature of space than Arithmetic throws on the population of the United States.
And Henri Poincaré added
What then are we to think of the question: Is Euclidean geometry true? It has no meaning. We might as well ask if the metric system is true and if the old weights and measures are false…One geometry cannot be more true than another; it can only be more convenient.
It is now generally believed that Newtonian mechanics and Euclidean geometry are how we tended to interpret the world with our minds, though they do not describe how the world ‘really’ is. Until the Nineteenth century, all of geometry could be deduced from the five postulates or axioms of Euclid. The first four are simple and elegant and were considered to be self-evident (a straight line can be drawn through any two points; a circle can be drawn around any point as its centre; lines can be extended indefinitely; all right angles are equal). The fifth, however, is inelegant (sometimes modified to a postulate about parallel lines, but Euclid’s postulate is more complex and general than that, involving interior angles between three lines) and doesn’t have the feel of being self-evident.
Euclid tried to avoid use of the fifth postulate unless absolutely essential, and he and most mathematicians until the Nineteenth century believed that its status could be rescued by showing that it could be deduced from the other four, so that geometry really rested on four self-evident postulates, although no-one had any lasting success in proving it. Those who tried to do geometry avoiding the use of the fifth postulate found the results so disconcerting and ‘absurd’ to the received view of reality that the enterprise was abandoned. Until the Nineteenth century, that is, when it was demonstrated that logically consistent non-Euclidean geometrical systems ‘existed’ if the fifth postulate was abandoned. There were howls of outrage, but this was largely damped down in the early Twentieth century when it was demonstrated that General Relativity, which was not dependent on Euclidean geometry, appeared to have empirical support.
There are a number of late Nineteenth and Twentieth century mathematical enterprises that should be mentioned. The first is Logicism, the enterprise in which Gottlob Frege attempted to reduce all of arithmetic to logic. Bertrand Russell exposed a fundamental flaw in Frege’s reasoning, but Russell (with A.N. Whitehead) then sought to demonstrate that not only arithmetic, but the whole of mathematics, including numbers themselves, could be deduced from logic. He took the first 362 pages in his Principia Mathematica to persuade the reader that he could demonstrate that 1 + 1 = 2.
Meanwhile there was Formalism, the enterprise of David Hilbert, to show that mathematics was not deduced (as Russell was attempting to prove) but was a logic game in which mathematicians defined the terms and set the rules. Hilbert declared
The fundamental idea of my proof theory is…to make a protocol of the rules by which our understanding actually proceeds…Already at this time I would like to assert what the outcome will be: mathematics is a presuppositionless science. To found it, I do not need God or the assumption of a special faculty of our understanding…
In 1900 Hilbert challenged formalist mathematicians to prove that mathematics was consistent and complete, and that it included a decision-making process for solving any problem.
Hilbert’s hopes were short lived. In 1931 Kurt Gödel showed that the consistency and completeness of any axiomatic system could not be proven – not even for arithmetic. He did so by using mathematical logic refined by Frege and Russell, together with the set theory of George Cantor, to prove that any axiomatic system necessarily generated statements that could not be proven to be either true or false within that axiomatic system (such as ‘this statement cannot be proven within this axiomatic system’ – a true but unproveable statement). By so doing he showed that no axiomatic system could be both consistent and complete.
Then in 1936 Alan Turing proved that no effective decision procedure existed for solving all problems in arithmetic, and thus for mathematics generally. He constructed his proof around the then imaginary ‘Turing machine’, the basis of the later digital computer, that acted on a fixed set of instructions, demonstrating that there were certain problems for which no algorithms could be written. Turing also proved the corollary, that a Turing machine could solve any logical or mathematical problem for which an algorithm could be written.
Then there is Conceptualism, or Intuitionism, which denies the extra-mental reality of universals as affirmed by the Realists, but also denies the analytic and formal nature of mathematics affirmed by the Nominalists. It is called Intuitionism because it affirms that mathematical judgments are a priori, intuitive and not empirically based. This view can be traced back to Immanuel Kant, but the main Twentieth century proponent was Luitzen Brouwer who even denied that the laws of logic have absolute validity and believed that mathematics was the mind imposing order on experience, such that there is no necessary connexion between mathematics and reality.
Some Nominalist mathematicians have been Fictionalists, in that they assert that mathematical statements are semantically true but strictly false, in the same way that the statement ‘Bilbo Baggins is a Hobbit’ is true in Tolkien fiction, but it is strictly false because there are no Hobbits in reality. As with other Nominalists, they deny the existence of abstract mathematical entities. Thus Fictionalists hold the statement ‘5 is greater than 3’ to be true semantically, but false in reality since ‘3’ and ‘5’ have no referents (as they do in ‘five loaves and three fishes’), and that likewise 1 + 1 = 2 is true in the narrative of mathematics, but false in reality.
But then we have the question of why mathematics seems to be so fertile, and why it appears to be essential to the scientific enterprise if there is no necessary connexion between mathematics and physical reality. Is it, in fact, possible to do science without mathematics? This question was answered by Hartry Field who in 1980 demonstrated the dispensability of mathematics to physics. Field, a Fictionalist, does not advocate doing science without mathematics, since he admits it is such a useful tool: he has chapters in his book Science Without Numbers: a Defence of Nominalism devoted to showing why mathematical entities are useful; but he demonstrated that physics is not dependent on mathematics and can be done apart from mathematics. He did so (using gravitational theory as an example) by avoiding the conventional approach of deriving a gravitational potential function, i.e. gravitational potential in terms of spacetime points (which commits one to realism about space, time, functions and real numbers). Field also proved a representation theorem such that his relational approach, which utilizes no gravitational potential functions, mass-density functions or spatio-temporal coordinate functions, can nevertheless recover all the relevant numerical claims if desired. In his chapter entitled My Strategy for Nominalizing Physics, and its Advantages he states concerning physical theories
Insofar as they’ve been rigorously formulated at all, they’ve been formulated platonistically, for it is easier to formulate a theory that way when one has a sufficiently developed mathematics…a thorough foundational analysis of such theories will show that reference to real numbers, etc. is no more necessary in them than it is in geometry.
Field’s work is under-appreciated, for it demonstrates that the mathematical conception of physical ‘laws’ may be based on ‘choice’ of how humans interpret the world and do science – a mathematical one. The so-called ‘laws of nature’ are then convenient fictions for the instrumental application of our interpretation of experience. Mathematics appears to reflect something of reality, not because it is actually intimately connected with physical reality, but because it is now our favoured instrument (or narrative, if you will) by which we interpret and express physical reality.
Of course, saying that mathematics is a metaphor, a narrative, an instrument etc for our interpretation of physical reality does not tell us whether mathematics has any separate ‘real’ existence of its own. Most mathematicians are Realists, as are many theologians; but, as shown above, some very influential mathematicians have been and are Nominalists, as are and have been many theologians. Many theists still cling to the Enlightenment/Deistic idea of ‘laws of nature’, but not all (Bas van Fraassen, for example), and some atheists deny ‘laws of nature’ because they believe it leads to the concept of a Deity (Nancy Cartwright, for example).
The big questions in mathematics don’t look as though they will be answered anytime soon.
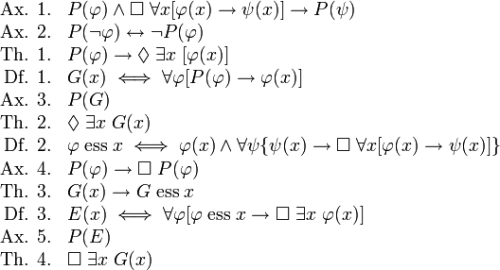
So have you examined James M. McCanney’s theory, or according to him, the solved problem of mathematics, -Calculate Primes- Direct Propagation of the prime numbers? McCanney calls it the oldest problem in mathematics, and that he has solved it. He claims that using a powerful new mathematical formula the prime numbers can now be directly calculated using only addition and subtraction starting with 0 and 1. He writes that, The solution technique may be applied to complex problems from quantum mechanics to genetics. He provides two books and a DVD on this subject. Have you heard of James, if so, I appreciate your thoughts on the matter he presents. {I’m not interested in challenging anyone, I’m simply a 53 year old student attempting to enjoy all that is possible around us within the limits of realism, and of course Creationism.} I find these blogs fascinating reads, all of them. Thanks.
ScientistForTruth responds
I have not studied McCanney. Thanks for the suggestion and the encouragement.
Hi
Thanks for an excellent blog. I don’t really understand all the math, but I get more or less what you’re saying.
I recently came across the concept of Biocentrism. From what I know and read about it its obviously fraught with controversy.
I would really like to know whether it should be taken seriously in the least.
I think your opinion and analysis of the subject would be great!
Biocentrism is a ‘new’ approach to the problem of the observer or consciousness in quantum theory. Championed by Robert Lanza. I’m sure you can find it in a jiffy if you haven’t already learned everything there is to know about it.
Thanks
ScientistForTruth replies
Thanks for your encouragement. I don’t know about Lanza – at a glance at some of his material it looks a bit way out. I’d have to study it to be able to give a fair critique.
Hi again
Well, there’s not much to study about Lanza. None of what he’s postulating has been said for the first time. 2 points of note.
1. The location of all objects is only within the brain as holograms (probably leading to the point that all sensory perception including touch is illusory -which, like you said, is waaay out.)
2. Space and time are modes of the animal mind through which we make sense of the universe
This by default shifts the focus onto biology rather than physics as the ultimate science that will provide the answer to the largest questions of existence.
I linked some things about that derivation by Gödel in a supplement to my joint article “An Interview With Kurt Gödel.”
Mathematics is a human artefact, a human conception, in which there is no truth … there is no absolute unity; no absolute space and no absolute time, there is no mathematics.
Gerrit Mannoury; (1867-1956); Quoted in Mystic, Geometer, and Intuitionist: The Life of L. E. J. Brouwer; Dirk van Dalen; 1999; p121